TOPIC 1 - What is computer hardware?
Digital Electronics
Silicon chip
- IC: Integrated Circuit - An electronic circuit on a small piece of semiconductor material performing the same function as larger circuits.
- Silicon chip: Integrated circuit which has millions of transistors connected by microscopic wires
- Die: A silicon wafer with hundreds of copies of the IC.
- Package: A container for the die which protects it from damage and connects it to the larger circuit. The die's pads are connected to the package pins.
Multicore processors
- Multiple independent cores put on the same IC sharing things like memory.
- Expensive but achieves better head dissipation and parallel computation.
- Allows for more computational power than a single core with a higher clock rate.
Moore's law
Moore's law says that we will double transistor capacity every 18-24 months. And this seems to be holding at least for now. Very soon we will have transistors the size of atoms and you can't get smaller than that.
Gates
- Transistors are built from gates.
- 0 = no voltage, 1 = high voltage
- Not gate, and gate, Or gate are the fundamental gates
See "Digital electronics" module for more info, as I don't want to repeat my notes.
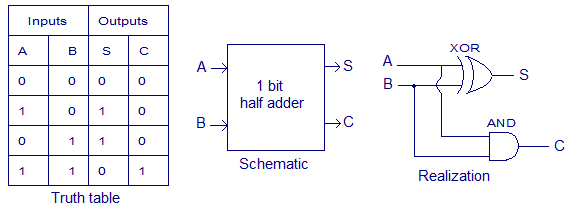
Half adder and full adder
To compute the sum of binary numbers we need an adder. We'll first look at the half adder then extend to the full adder.
Half Adder: This sums two binary inputs and creates a carry, if the inputs are 1 and 1. It does not except a carry as an input
- Uses the XOR for the sum since that has the desired truth table, carry only happens 1 AND 1, so an AND is used for that.
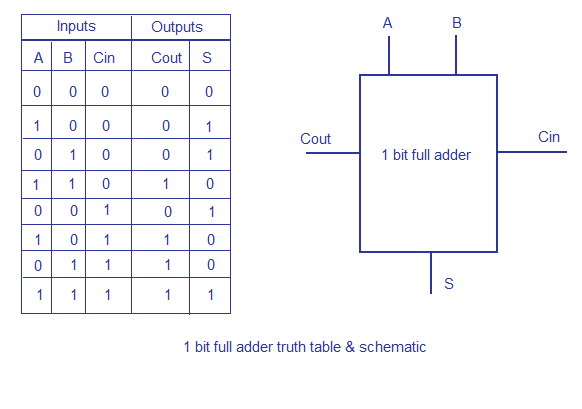
Full Adder: Like a half adder but also excepts a carry as an input and will add that to the sum
- This is the sum of the carry input and the sum of A and B, you need two half adders. if either half adder produces a carry the result will have a carry so an OR gate is used to compute the final carry.
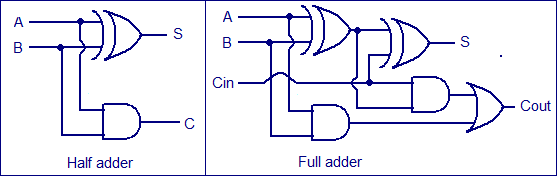
Summing multi-digit binary numbers
Now that we have a full adder the simplest way of summing two multi digit binary numbers is to create a chain of full adders where the sum of each digit is computed with the carry from the previous digit sum.
Machine Architecture
Pentium 4 processor microarchitecture
- Datapath: Aka the pipeline. This performs all the data processing operations, hence the name. Includes ALU and and a small amount of register memory.
- Control: Gives instructions to all the other parts
- Cache: On board memory for fast retrieval of data.
Von Neumann Architecture
This is the fundamental computer architecture and the key idea is the data and program are stored in the same place. This allows for cool self modifying programs.
Von Neumann Bottleneck: Limitation of the data transfer rate between CPU and memory. This was "fixed" by adding CPU (on-chip) caches, though Harvard architecture was the better fix.

Harvard architecture
This is another architecture where the data memory and instruction memory are stored separately, with separate buses for collecting the data. This solves the Van Neumann Bottleneck but means you can't have self modifying programs. However these days our computers use modified harvard architecture which is more complex and allows the processor to treat data as instructions and instructions as a data hence self modifying programs are again possible. We also kept the CPU caches from harvard architecture.
Memory
- Pigeon-hole: Memory is made of "Pigeon holes" holding addresses. Each "pigeon hole" holds 8 bits of data (1 byte)
- Words: These are 4 bytes combined together.
Buses
There are 3 types of buses, each used for a different purpose.
- Address Bus: Holds the addresses of locations in the memory. It's width must be large enough to hold even the largest address e.g 32 bits wide for 232 addresses.
- Data Bus: Carries the data of the memory. It's width determines how large the memory data can be.
- Control bus: Transfers information between the CPU and other devices within the process. Input/output, data being read/written.
Types of memory
| Type | Description | Cost | Speed |
| Hard Drive | Data stored off CPU, either on a rotating disk (HDD) or in semiconductor cells (SDD) | Cheap to create | Far from Cpu this makes it slow.C |
| Dynamic RAM | Data stored using transistors/capacitors | Cheap | Slow compared to static ram. Also capacitors must be refreshed every few seconds. |
| Static RAM | Data stored in flipflops, near CPU. | Expensive and takes up more space. | Stable and fast |
| Caches | Memory stored very close to CPU, as a buffer between the RAM and CPU. Stores frequently accessed items. Divided into two levels: - Level 1: Stored on CPU (registers, small space)
- Level 2: On or close to CPU (Cache), large space.
| Expensive. | Very fast. Level 1 is faster than level 2. |
Simple Von Neumann Processor
- Registers store program and data
- Accumulator stores arithmetic results
- Program counter (PC) holds next address
- Operations performed using fetch-decode-fetch-execute cycle.
- Read PC to get instruction address and fetch instruction
- Decode the instruction and increment the PC.
- If instruction needs operand Data then that is fetched.
- Execute the instruction and if necessary update PC.
For more information review your "machine architecture" notes.
Multi-core Computing
- More than one processor
- Either shared memory or distributed memory (this means processors are connected by a network)
- It's slower than two regular processors, but it allows for parallel processors and cheaper large scale computing devices.
General purpose graphic processing units (GPGPU)
- This is the idea of using the GPU's parallel computing abilities (see Machine architecture) for things other than graphics
- Can be a lot faster than CPU if the program is designed to work well with the GPU's limitations.
Instruction Set Architecture and MIPS
Instruction set architecture (ISA)
The instruction set architecture is basically the design of the instructions which allows the programmer to control the hardware. Alot of specific design choices are considered when making an instruction set architecture.
The ISA describes the:
- Structure of memory
- Instruction set formats
- Modes of addressing and accessing data
- How the process is executed
MIPS assembly language
This next part is going to overlap alot with machine architecture so i'll just touch on the essentials.
MIPS assumes:
- 232 memory locations
- Requesting an address returns the data of four addresses
- Only request addresses in intervals of 4
- Makes it so that all address are essentially 1 word or 32 bits wide
- The are 32 bit registers named $zero, $s1, $s2 ... $s7
Some examples of common MIPS assembly instructions:
| instruction | opcode and fields | Meaning |
| Load word | LW $t1 , ({offset}) $s | Loads a word from the source + offset to destination |
| Add intermediate | ADDI $t1, $s1, imm | Loads a word from Source adds the intermediate and puts in destination |
| Branch Equal | BEQ $s1, $s2, label | If source 1 == source 2, increase PC by the PC offset + 4 |
| Set less than | SLT $t1, $s1, $s2 | If source 1 < Source 2, set Dest to 1 else 0. |
| Jump | j label | Go to the target address |
| Halt | HLT | Stops the program |
Types of MIPS instructions
When making an instruction architecture you want a way of standardising the format of the instructions to reduce the circuit complexity, and make programming easier. MIPS is a RISC language which means it has very few instructions and only 3 formats.

| Type | Format | Example instructions |
| I-Type (Intermediate and register) | (Opcode, Rs, Rd, Imm) Bits: 6, 5, 5, 16 - Opcode = instruction code
- Rs = Source register
- Rd = Destination Register
- imm = memory address or intermediate constant
| |
| R-Type (Values all in registers) | (Opcode, Rs1, Rs2, Rd, shift, funct) Bits: 6, 5, 5, 5, 5, 6 - Opcode = instruction code (000000)
- Rs1 = Source register 1
- Rs2 = Source register 2
- Rd = Destination Register
- Shift = Shift value for shift instructions
- Funct = Supplement for opcode
| |
| J-Type (jump instructions) | (Opcode, Address) Bits: 6, 26 - Opcode = Instruction code
- Address = Location to jump to
| |
Operating systems
What are operating systems?
The operating system is the interface between the computer user and the computer hardware.
Kernel: Main component of OS, which loaded at boot time. It has full control of the CPU.
The main functions of the OS are:
- Virtualisation
- Creates virtual representations of complex hardware to make it easier for programs to control.
- Starts and stops programs
- Makes sure when programs stop memory is freed and stops programs when they crash
- Manages memory
- Hides the actual memory locations and prevents programs interfering with each others memory.
- Handles input/output
- Coordinates different input output activities and prevents them interpreting the main program
- Maintains file system
- Prevents programs accessing other programs data (Data-security) and allows accessing files in a structured way
- Networking
- Controls sending and receiving of data and provides some security over that data.
- Error handling
- Limits problems when programs don't do what they should allows recovery of data.
Input/Output
Examples of Input/output devices: Hard disk, CD, Graphics card, sound card, ethernet card, modem
These are connected to the cpu via a bus. However Buses are slow and if we had to pause the execution of the whole cpu to wait for an input to be received or output to be sent, it would causes a bottleneck. To solve this the operating system has Interrupts.
Interrupts: A signal to the cpu that input or output device has sent something on the bus. An interrupt handler announces thse signals to the CPU so that it can process it, then it resumes the paused process.
Processes
These are programs currently being executed. They consist of one or more thread(s) of instructions and an Address Space
- Thread(s): Sequence(s) of instructions in a sequential execution
- Address Space: Memory locations dedicated to the process for reading and writing.
Mutual exclusion: A property of processes which is says that no two threads can run the critical section at the same time. Where the critical section is a part of the program which accesses the same shared resource.
You can imagine a scenario where two threads had access to the same counter variable and changed it in some way. But if they ran at the same time one thread would change the counter accessed by the other thread causing all sorts of problems. This is why there must be mutual exclusion
Process life-cycle
The life cycle of a process is quite intuitive. It gets created, it waits for it's turn to run, it's gets run, then it stops. In addition it can also wait for other events. Each of these states has an equally intuitive name.
- New: Process is being created
- Ready: Process ready to be executed by the CPU
- Running: Process is being executed
- Blocked: The process stops running to wait for an event.
- Exit: Process ends
The actions done to move a process between these states also have special, harder to memorize, names that we have to learn because it makes it easier to communicate what the OS is doing to people.
- New -> Ready = Admit
- Ready -> Running = Dispatch
- Running -> Blocked = Event wait
- Blocked -> Running = Event
- Running -> Exit = Release
- Running -> Ready = Timeout/yield (this happens when a process decides or is forced to stop using the cpu)
Process control block
This is a container of information (data structure) used by the kernel to mange the processes. It contains all the information you could possibly need to know about it. Such as:
- ID
- State
- CPU Scheduling info
- Program counter
- for paused processes so they know where to resume
- Values in other CPU registers
- For paused processes so they data when they resume
- Memory management info
- Scheduling accounting info
- Like when it was last run and how much time it used.
Context switching
If you want processes to run in parallel you need to let them share the CPU space at the same time. Now this isn't possible, so we'll go with the next best thing: Context Switching.
This is where we periodically pause the execution of a process save all the necessary data needed for resuming to a PCB in the OS, then later after the other processes have had their turn, we resume it using the stored PCB data.
Note: This is time consuming and so it's why pc's have multiple cores so that processes can run in parallel for real without this added overhead.

TOPIC 2 - Fundamental problems
Introduction to problems in Computer Science
What is a computer science problem?
Unlike the more traditional subjects, Computer science problems are all about what method is used to achieve a goal and how good of a method it is, rather than just can you achieve the goal.
Problem in computer science are defined by:
- Constructive nature - How the solutions's can be put together to achieve the goal
- Repeated application - How applying a solution over and over is able to achieve the goal.
- Measurement of difficulty - We are concerned with how difficult it is to solve the problems and we measure/quantify this difficulty.
The essential notions of computer science
Computer science at it's core really just boils down to doing Computations with limited Resources and with Correctness
In most contexts Resources are the time or memory used by the computations and uses, and Correctness refers to if the solution is actually answers the problem (or in the case of optimisation: if it is the best answer to the problem)
Abstraction
This is where you take a real world problem and transform it into an idealised (mathematical) version which can be understood by a computer but also where the solution to this new variation can still be used to give the answer to the original real world problem.
Abstracting the travelling salesman problem
To understand abstraction a bit better lets take a look at how we can apply it to the travelling salesman problem (TSP).
The TSP is where a salesman wishes to find the shortest tour of a given collection of cities. (So that he saves as much time/fuel as possible.) To solve this we need to find a way of abstracting the real world problem into something we can obtain a computational solution for. We can do this with the following steps
| Steps | TSP example |
| Identify problem | Find shortest tour (by time) of a given collection of cities. |
| identify core information needed | - Start city
- Number of cities
- Distance between cities
|
| Create initial abstraction | Represent cities and distances as a weighted graph then the problem is equivalent finding the shortest hamolian cycle. |
| identify other considerations and abstractions for them | - Cities not known until visited
- Use queue of incoming cities
- If distance measured in time then it might vary with traffic or if distance is euclidean distance, actual time taken may vary.
- Represent distance as a function
- What if some city-to.city trips aren't possible.
- Represent distance as infinity.
|
| Consider trade off between quality and cost of obtaining solution | A solution which does not take into account the above considerations may be computable faster but may be less relevant to the real-world problem. |
Types of problems in computer science
Decision problems
This is a problem which asks a question about a given thing and the answer is either yes or no.
Common features:
- Set of possible instances
- Each instance either gives the answer "yes" or "no" with regards to a decision question
- We need to determine this answer.
Examples of decision problems and their abstractions
| Real-world problem | Description of problem | Abstraction | Other applications |
| Map colouring | Given a plane map of regions with each contained within a continuous border can you colour the map with k number of colours where no two adjacent regions have the same colour? | Since all the information is contained within which regions touch each other we can abstract it as a graph colouring problem Graph G = (V,E) where v is a set of vertices and E is a set of connecting edges. Colour the graph such that all pair of vertices joined by an edge are coloured differently. | Scheduling, register allocation, radio frequency assignment |
| Draughts | Given an n x n board of Draughts and a legal position of white and black checkers, where you play black and it's my go, can you still win from that position? | Abstract as a tree of all possible future positions, and determine if at least one leaf node is white. (Aka a win by white) | Chess, Go |
Search problems
This is a problem where you have lots of possible solutions for a given input and you need to return one. If there is no solution you need to say so.
Common features:
- Set of possible instances
- Set of possible solutions
- A binary search relation (a mapping between instances and the solutions)
To solve we a search where we are given an instance we need to find a solution from the possible solutions that fits the search relation for that instance. (or in plain english the solution needs to fit the criteria). Else there is no solution and we return "False".
Examples of search problems and their abstractions
| Real-world problem | Description of problem | Abstraction | Other applications |
| Sorting lists | Given a list of items like name or numbers where some items may be repeated, give one way of sorting them so they are in some fixed ordering. (e.g numeric or alphanumeric) | Abstract to a list of symbols. However, must consider that in the case of lists of lists, the data structures will be more complex | Telephone directory, File structure |
| Finding routes | Given a map and two locations can you find a route from point A to B, while also avoiding motorways? | Abstract to: - A graph where vertices are towns on the map and the edges are routes between towns which don't pass through other towns.
- List of motorways.
- Start and end towns
| Chess, Go |
Optimisation problems
These are problems where you have lots of possible solutions for a given input and you need to return the best one according to some criteria.
Common features:
- Set of instances
- Each instance has a set of solutions
- Each solution has a value of quality
- You need to return the "best" solution
Examples of optimisation problems and their abstractions
| Real-world problem | Description of problem | Abstraction | Other applications |
| Travelling salesman problem | Given a collection of cities and the distance between pairs of cities find the length of the shortest tour of cities where each visited exactly once. | Abstract to a weighted graph. (use abstraction described in detail earlier) | Telephone directory, File structure |
| Sports day | Given sports day events that must be scheduled at various times throughout the day, where each event takes 30 minutes and certain events can occur at the same time as long as the athletes are available what is the earliest time sports day can finish if there is the maximum number of events in the noon slot | Abstract to: - Graph where vertices are events and edges are events that cannot occur at the same time.
- Noon slot will have the largest group of vertices where no vertice is joined by an edge with any other vertice.
- The remaining slots are found by finding the minimal colouring of the remaining vertices, and assigning each colour to be a slot.
| Scheduling |
Methods to Solve Some Fundamental Problems
After abstracting a problem we then need an algorithm to solve that problem. We'll look at some different algorithms which exist for some of the fundamental computer science problems.
Algorithm: a process or set of rules to be followed in calculations or other problem-solving operations, especially by a computer.
Greedy algorithm: An algorithm which makes choices based on what look best in the moment. (finds the local optimum but not the global)
Colouring maps (Graph colouring)
We can abstract this as a Graph colouring problem, where the vertices are regions of the map and edges are adjacent regions.
We'll look at two different algorithms greedy colouring and point removal (brute force)
- Greedy colouring
- Pick a vertice, and choose the lowest colour not used by it's neighbours. Then move to the neighbours and repeat
- Does not always find the lowest number of colours and will give a different result depending on the order you pick vertices.
- Point removal
- Pick a and if it has less than k neighbours remove it from the graph, because no matter how the rest of the graph is coloured you could always extend it to that vertex by colouring a different colour to its neighbours.
- Keep going until you get to a graph with k colours. This can be trivially coloured.
- Always pick the vertex of smallest degree.
- If you can't remove any more points and the remaining number of points is not less than k, the graph cannot be k-coloured.
- At the end rebuild the set in the order that you removed them, assigning the lowest colour at each point.
Sports day (Maximum independent set + Graph colouring)
We abstract this as a graph where the vertices are the events and events which conflict are connected by edges. Then the largest number of events which can scheduled in one slot is equivalent to finding the maximum independent set of the vertices. To find a way of grouping the remaining events into slots we can treat it as a vertex graph colouring problem, and then assign each colour to a slot.
Note: Maximum ≠ maximal. Maximal independent set is a set which is not contained in any other set. However there may still be large independent sets, such as the maximum.
We'll look at a heuristic greedy algorithm for findinging a large independent set.
- Choose the vertex of smallest degree and put it into the independent set
- Remove it and its neighbours from the graph
- Go through the remaining vertices repeating the process until no vertex remains.
This algorithm works on the heuristic principle that if you remove as few vertices as possible at each step, you'll be able to create a large independent set. However whilst this will produce a large independent set it unfortunately does not produce the largest independent set. So it is still just a greedy algorithm
Finding tours in the TSP
We abstract the TSP as a weighted graph, and proceed to find the shortest cycle where each node is visited once. (Hamiltonian cycle)
A short but not optimally short path can be found with a greedy algorithm:
- Start at a random city.
- Pick the nearest unvisited city. (neighbour node with lowest edge weight.)
- Repeat until visited every city
- Output resulting tour.
Describing Algorithms
In Order to allow algorithms to be able to be described in a way which is sufficiently precise so that it can be programmed and analysed but still flexible enough that it can be used in any programming language, we will write them in a special language called Pseduo-code.
When it comes to algorithms we may be interested in proving:
- Correctness - does it get the right solution?
- Time complexity - How long does it take to get the solution?
Programming languages and paradigms
Programming languages vs algorithms
A programming language provides a way of translating an algorithm into a form, called a program, which can be executed by the computer.
Note: Algorithm ≠ Computer program. Whilst a program is concertely and explicitly defined in the programming language the algorithm can have many different implementations. Not only are there different implementations for each programming language but even with the same one there different implementations.
Programming paradigms
Programming paradigm: a way to classify programming languages based on their features.
There are lots and lots of paradigms, that people have come up with to group languages together but we'll just look at the most common.
- Imperative: Programmer tells the program how to change state (as in the state of variables in the program)
- Procedural: groups instructions into procedures. E.g functions.
- Object orientated: groups instructions into which part of the state they operate on.
- Declarative: Programmers declare what properties the final result will have but not how to compute it.
- Functional: Desired result is declared as the value of a series of function applications
- Logic: Desired result is declared as the answer to a question about a system of facts and rules.
- Data orientated: Programs work data by manipulating and searching relations (aka tables of data)
- Scripting: Programs automate the execution of tasks, to external programs. E.g javascript
- Assembly: Low level programs designed for specific processors. The interface between machine code and high level programs.
- Concurrent: Provides facilities for concurrency.
- Dataflow: models a program as a directed graph of the data flowing between operations
- Fourth-generation: Designed with a specific purpose in mind and to be as easy as possible. Often used to manipulate databases. E.g SQL.
- List-based: Programs based on the list structure (or rather lambda calculus). E.g Lisp.
- Visual: Allows users to create programs using graphic elements instead of text. E.g Scratch or Piet
Why are programming languages evolving?
Aliasing: Situation where the same memory location can be accessed by different pointers (names). Some people think this is a dangerous feature
- Productivity - Write code faster with less lines.
- Reliability - Enhance error detection with features like type-checking, exception handline and prevent aliasing
- Security - Make programing languages more trust worthy
- Execution speed - make programming languages run faster on parallel/distributed computers
- Style - Not sure about this one, but apparently programs are evolving to be more beautiful
Syntax and semantics
Syntax: Rules which tell us what can or can't be written in a programming language.
Semantics: Proving with formality what a program means.
Formally defining the semantics of a programming language should be done for the following reasons:
- Lets us prove that the program does what it should
- Means we can be sure it runs the same on different machines.
If we define semantics informally (like C, Fortran, python and many languages do) we can cause ambiguity which can cause errors.
There are different types of formal semantics we can use:
- Denotational: Denote programming elements with a mathematical structure.
- Operational: Give meaning in steps of operation taken by computation. E.g state changes
- Axiomatic: Look at how program changes some logical properties (based on axioms).
Compilers
Compilation vs interpretation
Compiled languages: The whole language is compiled at once into machine code.
Interpreted languages: Only one instruction at a time is translated to machine code and this is done during runtime.
| Advantages of Compiled languages | Advantages of Interpreted languages |
| Runs faster because not compiling during runtime. | Uses memory better since whole code does not need compiling |
| Can analyse code and optimise before runtime. | Faster development since there is zero compilation time. |
| Can avoid some runtime errors by finding bugs before runtime | |
Hybrid languages are also possible which combine compilation and interpretation to get the best of both worlds.
- Bytecode: a form of instruction set designed for efficient execution by a software interpreter. Programs can be compiled to this as an intermediate.
- Dynamic compilation: Semi compiles source program and fully compiles it when it's running in order to optimize for run-time libraries.
How does compilation work?
- Lexical analyser - Reads program and converts the characters to a sequence of basic components called tokens.
- Syntax analyser - represents the syntactic structure of the tokens as a parse tree.
- Translation - Flattens the parse tree into intermediate code (e.g bytecode), this is similar to assembly.
- Code generation - Translates the intermediate code into assembly and then into machine code.
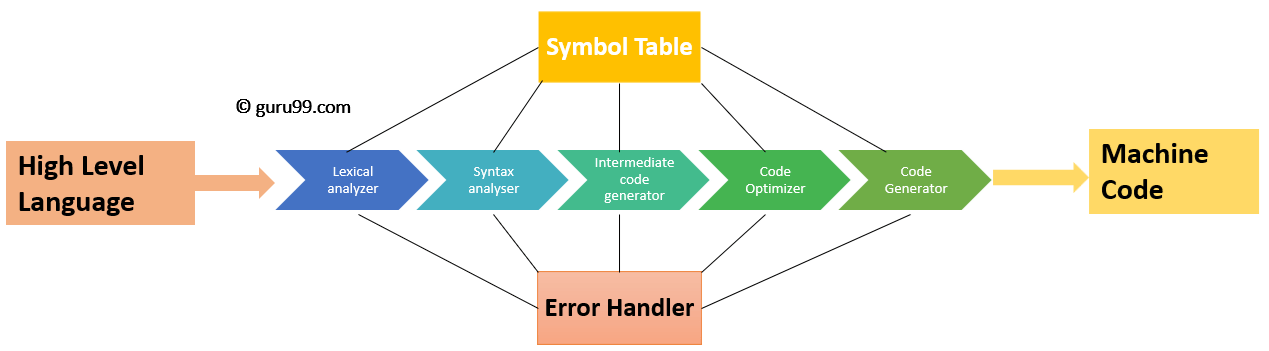
Lexical Analysis and Regular expressions
- Lexical analysis accounts for half of the compile time because handling characters is hard.
- In Order to extract tokens Regular expressions are used.
Regular expression: An expression which selects characters in the text from the alphabet
Some examples of regular expressions:
- a(a|b)*b = strings beginning with a and b with 0 containing only a's and b's
- (a|b)*(c(a|)*c(a|b)*)*(a|b)* = Strings beginning and ending with 0 or more a/b's with 0 or more caca's or cacb's.
Theorem: A string is denoted by a regular express iff it is accepted by a final state machine
Finite state machines
A finite state machine is a mathematical model of computation which can be in one of a finite number of states and can have it's state changed by inputs.
A finite state machine has:
- A finite alphabet ()
- A finite set of states with an initial state and final state (Q)
- And a transition function which tells it how to change state when it receives a specific input.
- A string is accepted by the FSM if after going through the transitions it ends up at the final state.
Pictorial representation of an FSM:
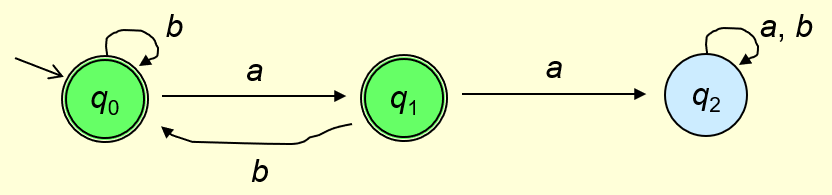
- The double ring circle are final states the single ring is not a final state.
- The arrows shows what happens to certain letters.
- You feed in the letters from the string and if you end up in the final state the string is accepted.
- In this case if there are two consecutive a's you will end up in q2 which is not a final state, thus only accepts strings without two consecutive a's.
TOPIC 3 - Efficiency and complexity
Analysis of algorithms
Resources used by algorithms
- Time taken
- Memory to store program
- Memory to run program
- Ease of implementation
Measuring the time taken by an algorithm
We measure time taken by algorithm rather than measure time taken by the implementation because this way it doesn't vary according to the programming language, computer or the processor speed. Thus it is machine-independent
Fundamental assumptions of algorithms:
- Variable manipulation and operations on variables can be performed in a fixed number of units of time called c
- a unit of time is the amount of time it takes for one fetch-decode-fetch-execute cycle to run
- Any basic algorithmic operation can run in at most c units of time
basic operation: An operation that takes one FDFE cycle.
Time complexity
Worst-case time complexity: This is given as a function of n, the input size, and tells how many units of time c, it would take to run the algorithm in the worst case. It is expressed as a function because if it was a constant then no matter what we picked we could find a value of n, for which the time surpassed that bound.
Big O notation: This lets us denote the worst-case time complexity and give an upper bound on the time.
Define precisely what we mean when we say that two functions f (n) : N → N and g(n) : N → N are such that f = O(g). [2]
There exists some n ∈ N and some positive rational k ∈ Q such that f(n) ≤ kg(n) whenever n ≥ n0.
Complexity and hardness
Complexity classes compared
Efficiently checkable/solvable: Can be checked/solved in polynomial time
Polynomial-time reduction: A polynomial time algorithm to convert one decision problem into another. where if one is true the other must also be true.
| Symbol | Complexity class | Meaning | Examples |
| P | (Deterministic) polynomial time | solvable in polynomial time. (tractable) | Sorting lists |
| NP | Non-deterministic polynomial time | Checkable in polynomial time, but not solvable (intractable) | - Decision version TSP
- Decision version graph colouring
- Decision version independent set
|
| NP-complete | A problem which can be reduced through a polynomial-time reduction into any NP problem and is in NP | |
| NP-hard | A problem which can be reduced into any NP problem with a polynomial-time reduction. (NP complete is a subset of NP-hard) | - optimisation version of TSP
|

P = NP
This is a famous unsolved computer science problem which attempts to show if a problem can be checked in polynomial time to can be solved in polynomial time. Suspected to be false.
- if Y is an NP-complete problem then P=NP is true if and only if Y ∈ P.
- because if all problems in NP must be part of P so P=NP
- If Y is a NP-hard problem then if Y can be solved in polynomial time then P=NP
Dealing with NP-hardness
Brute force
This is the idea of relying on computing power instead of intelligence by using a naive method to find all possible instances and pick the best/correct one.
Heuristic methods
- Genetic algorithms: Heuristicly solves optimisation problems by randomly generating possible instances and "breeding" the best instances and repeating. Based on principles of evolution.
- Any Colony Optimisation (ACO): "Artificial ants" traverse paths in a weighted graph leaving
View count: 1053